LASSO, sutrumpintai mažiausiai absoliutaus susitraukimo ir pasirinkimo operatorius, yra statistinė formulė, kurios pagrindinis tikslas yra duomenų modelių funkcijų parinkimas ir reguliavimas. Pirmą kartą šį metodą 1996 m. Pristatė statistikos profesorius Robertas Tibshirani. LASSO pateikia modelio sumos parametrus, suteikdamas jam viršutinę ribą, kuri veikia kaip suvaržymas sumai įtraukti absoliučius parametrus į leistiną diapazoną.
LASSO metodas reguliuoja modelio parametrus, sumažindamas regresijos koeficientus, kai kuriuos iš jų sumažindamas iki nulio. Funkcijos pasirinkimo fazė įvyksta po susitraukimo, kai kiekviena ne nulio reikšmė yra pasirinkta naudoti modelyje. Šis metodas yra reikšmingas siekiant sumažinti statistikos modeliuose paplitusias prognozavimo klaidas. Kiekybinė analizė Kiekybinė analizė yra išmatuojamų ir patikrinamų duomenų, tokių kaip pajamos, rinkos dalis ir darbo užmokestis, rinkimo ir vertinimo procesas, siekiant suprasti verslo. Duomenų technologijos laikais kiekybinė analizė yra laikoma pageidaujamu požiūriu priimant pagrįstus sprendimus. .
LASSO siūlo modelius su dideliu prognozavimo tikslumu. Tikslumas didėja, nes metodas apima koeficientų mažėjimą, o tai sumažina dispersiją ir sumažina šališkumą. Tai geriausiai veikia, kai stebėjimų skaičius yra mažas, o funkcijų skaičius yra didelis. Tai labai priklauso nuo λ parametro, kuris yra kontrolinis susitraukimo faktorius. Kuo didesnis tampa λ, tuo daugiau koeficientų verčiamas nuliui.
Kai λ yra lygus nuliui, tada modelis tampa įprasto mažiausių kvadratų regresija. Taigi, padidėjus λ, dispersija žymiai sumažėja, o rezultato šališkumas taip pat padidėja. „Lasso“ taip pat yra naudinga priemonė pašalinant visus kintamuosius, kurie nėra svarbūs ir kurie nėra susiję su atsako kintamuoju.
LASSO statistiniuose tiesiniuose modeliuose
Statistinis modelis yra realus matematinis problemos vaizdavimas. Modelis turėtų kuo labiau išreikšti problemą realiame pasaulyje, tuo pačiu padarydamas ją paprastą ir lengvai suprantamą. Modelį sudaro aiškinamieji ir atsako kintamieji.
aiškinamasis kintamasis yra nepriklausomas kintamasis, kuris priklauso tyrėjo nuožiūra. Nepriklausomi kintamieji yra modelio įvestys, kurias tyrėjas gali išmatuoti, norėdamas nustatyti jų poveikį modelio rezultatams.
atsako kintamasis yra priklausomas kintamasis Priklausomas kintamasis Priklausomas kintamasis yra tas, kuris pasikeis priklausomai nuo kito kintamojo, vadinamo nepriklausomu kintamuoju, vertės. tai yra pagrindinis eksperimento akcentas. Tai sudaro eksperimento rezultatą, kuris gali būti vienas rezultatas, jei tai yra vienkrypčiai modeliai, arba, jei tai daugiamatis modelis, - keli rezultatai.
LASSO yra neatsiejama modelio kūrimo proceso dalis, ypač naudojant funkcijų pasirinkimą. Funkcijų pasirinkimo etapas padeda pasirinkti aiškinamuosius kintamuosius, kurie yra nepriklausomi kintamieji, taigi ir modelio įvestiniai kintamieji.
Įvesties kintamieji yra svarbūs elementai, lemiantys modelio išvestį ir padedantys įvertinti jų poveikį atsako kintamiesiems. Tinkamų kintamųjų pasirinkimas lemia modelio tikslumą. LASSO funkcijų pasirinkimo etapas padeda tinkamai parinkti kintamuosius.
Įvertinimas su LASSO
Statistiniai modeliai remiasi LASSO tiksliam kintamųjų pasirinkimui ir reguliavimui. Tiesinės regresijos regresijos analizėje regresijos analizė yra statistinių metodų rinkinys, naudojamas sąryšiui tarp priklausomo kintamojo ir vieno ar daugiau nepriklausomų kintamųjų įvertinti. Jis gali būti naudojamas vertinant santykio tarp kintamųjų stiprumą ir modeliuojant būsimą jų santykį. , pavyzdžiui, LASSO įveda viršutinę kvadratų sumos ribą, taigi sumažina modelio klaidas. LASSO įvertis priklauso nuo parametro λ.
Parametras λ kontroliuoja susitraukimo stiprumą, kai padidėjus λ, padidėja susitraukimas. Visų koeficientų sumos viršutinė riba yra atvirkščiai proporcinga parametrui λ. Kai viršutinė riba padidėja, parametras λ mažėja. Kai viršutinė riba mažėja, parametras λ tuo pačiu didėja.
Kai viršutinė riba didėja link begalybės, parametras λ artėja prie nulio, todėl eksperimentas paverčiamas paprastais mažiausiais kvadratais, kur parametras λ visada lygus nuliui. Kai viršutinės ribos koeficientai artėja prie nulio, parametro λ vertė didėja link begalybės.
LASSO geometrija
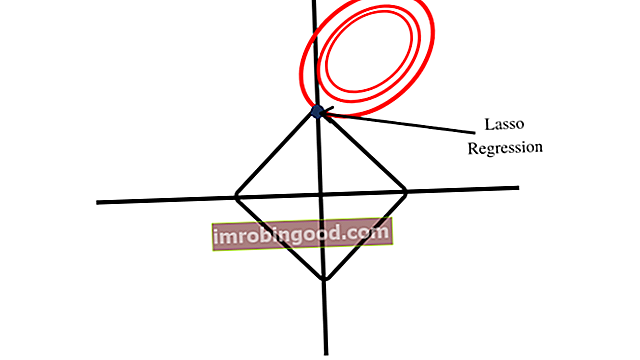
LASSO suformuoja deimanto formą savo suvaržymo srityje, kaip parodyta paveikslėlyje žemiau. Deimanto forma apima kampus, skirtingai nuo apskritimo formos, susidariusios dėl kraigo regresijos. Pirmojo taško artumas prie kampo rodo, kad modelis turi vieną koeficientą, kuris yra lygus nuliui.
Keterų regresijos suvaržymų sritis suformuoja apskritimo formą, kurioje nėra kampų, panašių į tuos, kuriuos suformuoja LASSO suvaržymų sritis, kai braižoma. Todėl kraigo regresijos koeficientai negali būti lygūs nuliui.
Svertinis LASSO
Svertinis LASSO yra rezultatas, kai tyrėjas atskirai baudžia regresijos koeficientus. Tai reiškia, kad užuot taikius visiems koeficientams bendrą parametrą λ, koeficientai baudžiami atskirai, naudojant skirtingus parametrus.
Svorius galima nustatyti naudojant LASSO algoritmą, kad svoriai būtų tinkamai priskirti tiksliam modeliavimui. Panašus regresijos koeficientų svoris yra kooperatyvas LASSO, kur už koeficientus baudžiama grupėse, kurios laikomos panašiomis.
Papildomi resursai
Finansai yra oficialus sertifikuoto bankų ir kreditų analitiko (CBCA) ™ CBCA ™ sertifikavimo teikėjas. Sertifikuoto bankų ir kreditų analitiko (CBCA) ™ akreditacija yra pasaulinis kredito analitikų standartas, apimantis finansus, apskaitą, kredito analizę, pinigų srautų analizę sandoros modeliavimas, paskolos grąžinimas ir kt. sertifikavimo programa, skirta visiems paversti pasaulinio lygio finansų analitikais.
Norėdami toliau mokytis ir tobulinti savo žinias apie finansinę analizę, labai rekomenduojame toliau pateiktus papildomus finansų išteklius:
- Prognozavimo metodai Prognozavimo metodai Į viršų Prognozavimo metodai. Šiame straipsnyje paaiškinsime keturių rūšių pajamų prognozavimo metodus, kuriuos finansų analitikai naudoja prognozuodami būsimas pajamas.
- Nepriklausomas kintamasis Nepriklausomas kintamasis Nepriklausomas kintamasis yra įvestis, prielaida ar tvarkyklė, kuri pakeista siekiant įvertinti jo poveikį priklausomam kintamajam (rezultatui).
- Daugkartinė tiesinė regresija Daugkartinė tiesinė regresija Daugkartinė tiesinė regresija reiškia statistinę metodiką, naudojamą prognozuoti priklausomo kintamojo rezultatą, remiantis nepriklausomų kintamųjų verte.
- Scenarijų analizė Scenarijų analizė Scenarijų analizė yra metodas, naudojamas analizuoti sprendimus spekuliuojant įvairius galimus finansinių investicijų rezultatus. Finansiniame modeliavime tai

