Koreguotas R kvadratas yra modifikuota R kvadrato versija, kuri atspindi prognozuotojus, kurie nėra reikšmingi regresijos modelyje. Kitaip tariant, pakoreguotas R kvadratas parodo, ar pridedant papildomų numatiklių pagerėja regresijos modelis, ar ne. Norint suprasti pakoreguotą R kvadratą, reikia suprasti R kvadratą.
Santrauka:
- Koreguotas R kvadratas yra modifikuota R kvadrato versija, pritaikoma prognozuotojams, kurie nėra reikšmingi regresijos modelyje.
- Palyginti su modeliu su papildomais įvesties kintamaisiais, mažesnis pakoreguotas R kvadratas rodo, kad papildomi įvesties kintamieji neprideda vertės modeliui.
- Palyginti su modeliu su papildomais įvesties kintamaisiais, didesnis pakoreguotas R kvadratas rodo, kad papildomi įvesties kintamieji prideda modelio vertės.
Kas yra R kvadratas?
R kvadratas, dar vadinamas determinacijos koeficientu, nustatymo koeficientas. Nustatymo koeficientas (R² arba r kvadratas) yra statistinis regresijos modelio matas, kuris nustato priklausomojo dispersijos dalį, naudojamas paaiškinti laipsnį iki kurie įvestiniai kintamieji (numatomieji kintamieji) paaiškina išvesties kintamųjų (numatomų kintamųjų) kitimą. Tai svyruoja nuo 0 iki 1. Pavyzdžiui, jei R kvadratas yra 0,9, tai rodo, kad 90% išvesties kintamųjų kitimo paaiškinama įvesties kintamaisiais. Paprastai tariant, didesnis R kvadratas rodo, kad modelis geriau tinka. Apsvarstykite šią schemą:
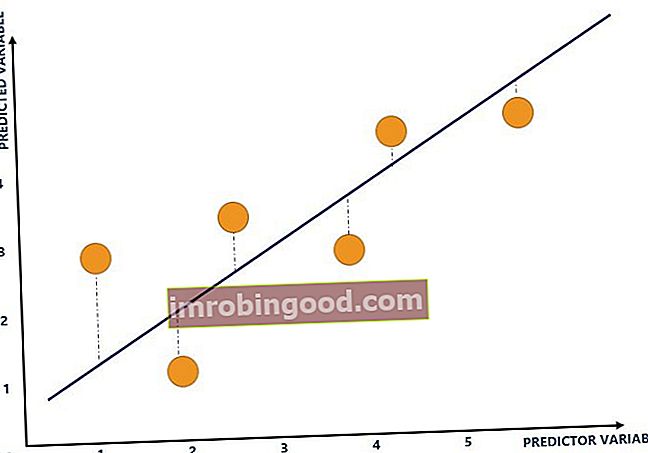
Mėlyna linija nurodo geriausiai tinkančią liniją ir parodo ryšį tarp kintamųjų. Linija apskaičiuojama atliekant regresijos analizę Regresijos analizė Regresijos analizė yra statistinių metodų rinkinys, naudojamas sąryšiui tarp priklausomo kintamojo ir vieno ar daugiau nepriklausomų kintamųjų įvertinti. Jis gali būti naudojamas vertinant santykio tarp kintamųjų stiprumą ir modeliuojant būsimą jų santykį. ir braižomas ten, kur yra kuo mažesni geltonų taškų vertikalūs atstumai (mėlynos punktyrinės linijos) iki geriausiai tinkančios linijos.
Geltoni taškai nurodo įvesties ir išvesties kintamųjų diagramą. Įvesties kintamasis yra nubrėžtas x ašyje, o išvesties kintamasis yra y ašyje. Pavyzdžiui, aukščiau pateiktą diagramą sudaro šis duomenų rinkinys:

Mėlynos punktyrinės linijos nurodo įvesties ir išvesties kintamųjų diagramos atstumą nuo geriausiai tinkančios linijos. R kvadratas gaunamas iš visų geltonų taškų atstumo nuo geriausiai tinkančios linijos (mėlynos linijos). Pvz., Šioje diagramoje pavaizduotas R kvadratas 1:

Problemos su R kvadratu
R kvadratas turi būdingą problemą - dėl papildomų įvesties kintamųjų R kvadratas išliks toks pats arba padidės (taip yra dėl to, kad R kvadratas apskaičiuojamas matematiškai). Todėl net jei papildomi įvesties kintamieji neturi ryšio su išvesties kintamaisiais, R kvadratas padidės. Toliau pateikiamas pavyzdys, paaiškinantis tokį įvykį.
Suprasti pakoreguotą R kvadratą
Iš esmės pakoreguotas R kvadratas nagrinėja, ar modelį papildo papildomi įvesties kintamieji. Apsvarstykite pavyzdį, naudodamiesi picos savininko surinktais duomenimis, kaip parodyta žemiau:
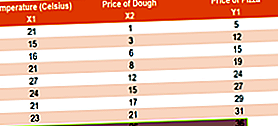
Tarkime, kad picos savininkas vykdo dvi regresijas:
1 regresija: tešlos kaina (įvesties kintamasis), picos kaina (kintamasis)
1 regresija duoda R kvadratą 0,9557 ir pakoreguotą R kvadratą 0,9493.
2 regresija: temperatūra (1 įvesties kintamasis), tešlos kaina (2 įvesties kintamasis), picos kaina (kintamasis kintamasis)
Regresija 2 duoda R kvadratą 0,9573 ir pakoreguotą R kvadratą 0,9431.
Nors temperatūra neturėtų daryti jokios prognozinės galios picos kainai, R kvadratas padidėjo nuo 0,9557 (1 regresija) iki 0,9573 (2 regresija). Asmuo gali tikėti, kad regresija 2 turi didesnę numatomąją galią, nes R kvadratas yra didesnis. Nors įvedant temperatūros kintamąjį nenaudojama prognozuojant picos kainą, jis padidino R kvadratą. Čia patenka pakoreguotas R kvadratas.
Koreguotas R kvadratas nagrinėja, ar prie modelio prisideda papildomi įvesties kintamieji. 1 regresijos koreguotas R kvadratas buvo 0,9493, palyginti su koreguotu R kvadratu 2 regresijoje iš 0,9493. Todėl pakoreguotas R kvadratas gali nustatyti, kad įvestas temperatūros kintamasis nėra naudingas paaiškinant produkcijos kintamąjį (picos kainą). Tokiu atveju pakoreguotas R kvadratas nurodys modelio kūrėją naudoti regresiją 1, o ne regresiją 2.
Koreguoto R kvadrato pavyzdys
Apsvarstykite du modelius:
- 1 modelyje prognozuojami Y1 naudojami įvesties kintamieji X1, X2 ir X3.
- 2 modelis naudoja įvesties kintamuosius X1 ir X2, kad numatytų Y1.
Kuris modelis turėtų būti naudojamas? Informacija apie abu modelius pateikiama toliau:

Lyginant R modelio 1 ir 2 modelio kvadratą, R kvadratas prognozuoja, kad 1 modelis yra geresnis modelis, nes jis turi didesnę aiškinamąją galią (0,5923 1 modelyje ir 0,5612 2 modelyje).
Palyginus R modelio 1 ir 2 modelio kvadratą, pakoreguotas R kvadratas prognozuoja, kad įvesties kintamasis X3 prisideda prie išėjimo kintamojo Y1 paaiškinimo (1 modelyje 0,4231, o 2 modelyje - 0,3512).
Taigi reikėtų naudoti 1 modelį, nes papildomas X3 įvesties kintamasis padeda paaiškinti išėjimo kintamąjį Y1.
Papildomi resursai
Finansai siūlo finansinio modeliavimo ir vertinimo analitikui (FMVA) ™ FMVA® atestaciją. Prisijunkite prie 350 600 ir daugiau studentų, dirbančių tokiose įmonėse kaip „Amazon“, J. P. Morganas ir „Ferrari“ sertifikavimo programa tiems, kurie nori pakelti savo karjerą į kitą lygį. Norint toliau mokytis ir tobulėti karjeroje, bus naudingi šie finansų ištekliai:
- Pagrindinės finansinės statistikos sąvokos Pagrindinės finansų statistikos sąvokos Tvirtas statistikos supratimas yra nepaprastai svarbus, kad padėtų mums geriau suprasti finansus. Be to, statistikos sąvokos gali padėti investuotojams stebėti
- Aukšto ir mažo metodo ir regresijos analizė Aukšto mažo metodo ir regresijos analizė Aukšto mažo metodo ir regresijos analizė yra du pagrindiniai sąnaudų vertinimo metodai, naudojami vertinant pastoviųjų ir kintamųjų sąnaudų sumas. Paprastai vadovai, norėdami numatyti ir planuoti ateitį, turi suskirstyti mišrius kaštus į fiksuotą ir kintamą komponentą.
- Nepriklausomas kintamasis Nepriklausomas kintamasis Nepriklausomas kintamasis yra įvestis, prielaida ar tvarkyklė, kuri pakeista siekiant įvertinti jo poveikį priklausomam kintamajam (rezultatui).
- Finansinės analizės rūšys Finansinės analizės rūšys Finansinė analizė apima finansinių duomenų naudojimą įmonės veiklos įvertinimui ir rekomendacijų, kaip ji galėtų pagerėti toliau. Finansų analitikai pirmiausia dirba „Excel“, naudodami skaičiuoklę, kad analizuotų istorinius duomenis ir sudarytų prognozes. Finansinės analizės tipai

