Ballpark figūra yra tikslus kintamojo vertės įvertinimas. Paprastai jis apskaičiuojamas naudojant paprastą apytikslį, o ne atliekant faktinį skaičiavimo procesą, kuris yra sudėtingesnis.

„Ballpark“ skaičiai pateikia pagrįstą įvertinimą, kai nėra sudėtingesnių įrankių, tokių kaip skaičiuoklės. Daugelis tokių apytikslių duomenų buvo plačiai naudojami, kol kompiuteriai tapo įprastu finansų sektoriuje.
Nepaisant šių dienų plačiai naudojamų kompiuterių, kamuolio aikštelės skaičiavimai tebėra naudojami. Įvertinimo metodų paprastumas padeda sumažinti skaičiavimo sudėtingumą. Tai padeda sumažinti klaidos tikimybę atliekant dešimtaines (slankiojo kablelio) operacijas, taip pat žmogišką klaidą, pavyzdžiui, įvedant neteisingą formulę.
Kituose skyriuose pamatysime įvairiose finansų srityse naudojamų kamuolių skaičių, pavyzdžiui, pinigų laiko vertę. Laiko pinigų vertę. Laiko pinigų vertė yra pagrindinė finansinė koncepcija, pagal kurią pinigai dabartyje yra verti daugiau nei ta pati pinigų suma, kurią reikia gauti ateityje. Tai tiesa, nes pinigus, kuriuos turite dabar, galite investuoti ir uždirbti grąžą, taip sukurdami didesnę pinigų sumą ateityje. (Be to, su ateitimi, išvestinėmis finansinėmis priemonėmis, nekilnojamuoju turtu ir kt.
Ballpark paveikslų pavyzdžiai
1. Laiko pinigų vertė
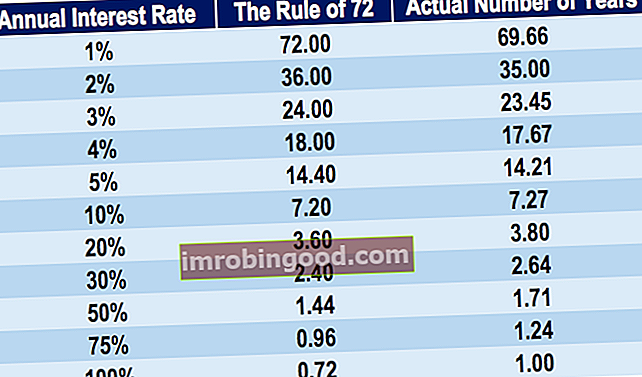
Dažniausias „Ballpark“ figūros panaudojimo pavyzdys yra iš pačių finansų pagrindų - 72 taisyklė 72 taisyklė Finansuose 72 taisyklė yra formulė, kuri apskaičiuoja laiką, kurio reikia investicijų vertės padvigubėjimui, uždirbdamas fiksuotą metinę grąžos normą. „Taisyklė 72“ yra spartusis klavišas arba voko atgalinis skaičiavimas, skirtas nustatyti, kiek laiko investicija gali padvigubėti. . Taisyklė tiesiog nurodo, kad norint apskaičiuoti, kiek laiko reikia dvigubai didesnėms investicijoms, pateikiama tokia paprasta formulė:

Kur:
- T - Laikas padvigubinti investicijas
- r - Palūkanų norma dešimtainiu pavidalu (taigi r = 0,1 10%)
Kaip parodyta toliau pateiktoje diagramoje, 72 taisyklė yra puikus įvertinimas, palyginti su faktine verte, apskaičiuota naudojant „NPER“ funkciją „NPER“ funkcija. „NPER“ funkcija yra suskirstyta į „Excel Financial“ funkcijas. Ši funkcija padeda apskaičiuoti periodų, kurių reikia norint išmokėti paskolą arba pasiekti investicinį tikslą, skaičių reguliariai mokant periodiškai ir taikant fiksuotą palūkanų normą. „Excel“.

Svarbu pažymėti, kad taisyklė taikoma, jei investicija apima tarpinius mokėjimus, pavyzdžiui, anuitetą. Taip yra todėl, kad didėjant mokėjimams, laikas, per kurį investicijos padvigubėja, krinta labai greitai.
2. Obligacijos
Obligacijos pateikiamos su visomis su jomis susijusiomis metrikomis. Viena tokių rodiklių yra obligacijų trukmė. Obligacijos trukmė yra jos kainos jautrumas pokyčiui pelningumo iki išpirkimo. Kalbant apie šio straipsnio taikymo sritį, mes pažvelgsime tik į tai, kaip jis apskaičiuojamas naudojant formulę, palyginti su trukmės įvertinimu.
Paprastos atkarpos obligacijos trukmei apskaičiuoti naudojama ši formulė:

Kur:
- y - Obligacijos grąžos terminas
- c - Kupono norma
- N - Likusių kuponų ar laikotarpių skaičius
- t - Dienos nuo paskutinio kupono
- T - Iš viso dienų kupono laikotarpiu
T ir T pasirinkimas priklauso nuo dienų skaičiavimo tvarkos, naudojamos vertinant. Trumpai tariant, tai labai sudėtinga, nes yra daug judančių dalių. Rutulio aikštės trukmės įvertis pateikiamas taikant paprastesnę procedūrą, aprašytą toliau:

Kur:
- MV (žemyn) - Obligacijos rinkos vertė, apskaičiuota mažinant dabartinę grąžą (∆y)
- MV (aukštyn) - Obligacijos rinkos vertė, apskaičiuota padidinus dabartinę pajamingumą nedidele suma (∆y)
- MV (pradinis) - Obligacijos rinkos vertė, apskaičiuota pagal dabartinį pelningumą
- ∆y - Maža suma, kuria pakeisite pajamingumą, kad atliktumėte aukščiau nurodytus skaičiavimus
Rinkos vertę galima lengvai apskaičiuoti naudojant „Excel“ funkciją „PV“, tada prijungiant vertes pagal anksčiau pateiktą formulę. Žemiau pateiktame paveikslėlyje apibendrinti du metodai ir jų rezultatai.

Skaičiavimą galima tiksliau sumažinti ∆y vertę kuo arčiau nulio arba patenkinamai tiksliai.
3. Akcijos
Vertinant akcijas dažniausiai naudojama diskonto norma yra vidutinė svertinė kapitalo kaina (WACC). WACC WACC yra įmonės vidutinė svertinė kapitalo kaina ir atspindi jos sumaišytą kapitalo kainą, įskaitant nuosavą kapitalą ir skolą. WACC formulė yra = (E / V x Re) + ((D / V x Rd) x (1-T)). Šiame vadove apžvelgiama, kas tai yra, kodėl jis naudojamas, kaip jį apskaičiuoti, taip pat pateikiama atsisiunčiama WACC skaičiuoklė. WACC apima daug įvesties duomenų, o kai kurie iš jų yra vertinami, o ne aiškiai apskaičiuojami. Du tokie įnašai yra beta ir akcijų rizikos premija (ERP), kuri naudojama apskaičiuojant nuosavo kapitalo kainą.
Yra daugybė būdų nustatyti beta versiją. Aiškus metodas yra reguliuoti akcijų grąžos ir rinkos grąžos regresiją. Tačiau tai lemia beta įverčių neatitikimus dėl naudojamų duomenų (dienos ar savaitės grąžos, istorijos trukmės ir kt.). Norint įveikti tokią problemą, norint apskaičiuoti beta versiją, naudojamas patikimų šaltinių palyginamų įmonės beta versijų vidurkis arba mediana.
Panašiai ERP atveju skaičiavimams atlikti naudojamas sutarimo įvertinimas, o ne statistinis darbas, kad būtų galima jį apskaičiuoti iš neapdorotų duomenų. Pavyzdžiui, maždaug 5% skaičius yra įprastas ERP rodiklis.
Aukščiau pateiktos idėjos iliustruojamos gerai cituojamoje apklausoje „Geriausia praktika vertinant kapitalo kainą“.
4. Dariniai
Išvestiniai finansiniai instrumentai yra plati disciplina ir siūlo daugybę būdų, kaip apskaičiuoti skirtingas kamuolio aikštės figūras, kai kurie yra sudėtingesni nei kiti. Du žemiau išvardyti metodai parodo, kaip apskaičiuoti kainą ir numanomą kviestinių pasirinkimo sandorių prie pinigų ar prie jų nepastovumą.
Pirkimo pasirinkimo kaina nurodoma pagal „Black-Scholes“ formulę. Tačiau yra lengvesnis būdas apskaičiuoti pasirinkimo kainą, kai ji artima pinigams. Apytikslė vertė remiasi „Black-Scholes“ sistema, kaip aprašyta toliau:

Kur:
- S - Pagrindinės priemonės kaina
- σ - Pagrindinių priemonių nepastovumas
- t - Laikas iki galiojimo pabaigos

Numanomas nepastovumas Numanomas nepastovumas (IV) Numanomas nepastovumas - arba tiesiog IV - naudoja pasirinkimo sandorio kainą, kad apskaičiuotų, ką rinka sako apie būsimą pasirinkimo sandorio nepastovumą, tai yra nepastovumo parametro vertė, kurią reiškia rinkos kaina pasirinkimo. Vertinant pasirinkimo galimybes svarbu atkreipti dėmesį į tai, kad galima pastebėti visus duomenis, išskyrus nepastovumą, kuris turi būti įvertintas. Taigi skirtumas tarp modelio kainos (tarkime, iš „Black-Scholes“ modelio) ir rinkos kainos yra susijęs su nepastovumu.
Norint apskaičiuoti numanomą nepastovumą, reikia naudoti kompiuterinę programą, kuri bandymų ir klaidų būdu atliktų teisingą numanomo nepastovumo vertę. Tačiau galima gauti netiesioginių pinigų pasirinkimo variantų netiesioginio kintamumo skaičių naudojant šią formulę:

Kur:
- C - Skambučio už pinigus kaina
- S - Pagrindinės priemonės kaina
- t - Laikas iki galiojimo pabaigos

5. Nekilnojamasis turtas
Panaši koncepcija kaip kamuolio aikštės figūra yra „voko atgal“ skaičiavimo koncepcija. Voko atgalinis skaičiavimas yra supaprastinta faktinio skaičiavimo versija, kuri suteikia reikiamo kintamojo įvertinimą rutulio aikštėje.
Dažnas tokio skaičiavimo pavyzdys yra nekilnojamojo turto sektoriaus viršutinės ribos apskaičiavimas. Yra sudėtingi modeliai, skirti nustatyti nuosavybės viršutinę ribą, tačiau tai galima įvertinti atlikus paprastą skaičiavimą, aprašytą toliau:

Atliekant pirmiau pateiktą skaičiavimą, viršutinės normos dydis apskaičiuojamas taip:

Grynosios veiklos pajamos gaunamos iš pagrindinių prielaidų ir faktų apie turtą. Tai supaprastintas išsamesnių pramonėje naudojamų modelių atvaizdavimas.
Susiję skaitymai
Finansai yra oficialus pasaulinio sertifikuoto bankų ir kreditų analitiko (CBCA) ™ CBCA ™ sertifikavimo teikėjas. Atestuota bankų ir kreditų analitikų (CBCA) ™ akreditacija yra pasaulinis kredito analitikų standartas, apimantis finansus, apskaitą, kredito analizę, pinigų srautų analizę. , sandorio modeliavimas, paskolos grąžinimas ir kt. sertifikavimo programa, skirta padėti visiems tapti pasaulinio lygio finansų analitikais. Norėdami toliau siekti karjeros, naudingi toliau nurodyti papildomi finansų ištekliai:
- Beta Beta Investicinio vertybinio popieriaus (t. Y. Akcijų) beta (β) yra jo grąžos nepastovumo, palyginti su visa rinka, matavimas. Jis naudojamas kaip rizikos matas ir yra neatsiejama kapitalo turto kainodaros modelio (CAPM) dalis. Didesnės beta versijos bendrovė turi didesnę riziką ir didesnę tikėtiną grąžą.
- „Black-Scholes-Merton“ modelis „Black-Scholes-Merton“ modelis „Black-Scholes-Merton“ (BSM) modelis yra finansinių priemonių kainodaros modelis. Jis naudojamas vertinant akcijų pasirinkimo sandorius. Modelis yra įpratęs
- Nuosavybės rizikos premija Nuosavybės rizikos premija Nuosavybės rizikos premija yra skirtumas tarp nuosavybės ar atskirų akcijų grąžos ir nerizikingos grąžos normos. Tai kompensacija investuotojui už prisiimtą didesnį rizikos lygį ir investavimą į akcijų, o ne nerizikingus vertybinius popierius.
- Nekilnojamojo turto finansinis modeliavimas Nekilnojamojo turto finansinis modeliavimas