Laiko pinigų vertė yra pagrindinė finansinė sąvoka, pagal kurią pinigai dabartyje yra verti daugiau nei ta pati pinigų suma, kurią reikia gauti ateityje. Tai tiesa, nes pinigus, kuriuos turite dabar, galite investuoti ir uždirbti grąžą, taip sukurdami didesnę pinigų sumą ateityje. (Be to, esant būsimiems pinigams, kyla papildoma rizika, kad pinigai dėl vienų ar kitų priežasčių niekada nebus gauti.) Piniginė laiko vertė kartais vadinama grynąja dabartine verte grynąja dabartine verte (NPV) grynąja dabartine verte. Vertė (NPV) yra visų būsimų pinigų srautų (teigiamų ir neigiamų) vertė per visą investicijos galiojimo laiką, diskontuota iki šiol. NPV analizė yra savaiminio vertinimo forma ir yra plačiai naudojama finansų ir apskaitos srityse nustatant verslo vertę, investicijų vertybinius popierius (NPV).
Kaip veikia pinigų laiko vertė
Paprastas pavyzdys gali būti naudojamas parodyti pinigų laiko vertę. Tarkime, kad kažkas siūlo jums sumokėti vienu iš dviejų būdų už tam tikrą darbą, kurį atliekate dėl jų: jis arba sumokės jums 1 000 USD dabar, arba 1100 USD po vienerių metų.
Kurį atlyginimo variantą turėtumėte pasirinkti? Tai priklauso nuo to, kokios investicijos grąžos grąžos norma Grąžos norma (ROR) yra investicijos pelnas ar nuostolis per tam tikrą laikotarpį, lyginant su pradinėmis investicijos sąnaudomis, išreikštomis procentais. Šis vadovas moko dažniausiai naudojamų formulių, kurias galite uždirbti iš pinigų šiuo metu. Kadangi 1100 USD yra 110% nuo 1000 USD, tada, jei manote, kad investuodami pinigus per ateinančius metus galite uždirbti daugiau nei 10% pinigų, turėtumėte nuspręsti pasinaudoti 1000 USD dabar. Kita vertus, jei nemanote, kad investuodami pinigus kitais metais galėtumėte uždirbti daugiau nei 9%, tuomet turėtumėte sumokėti būsimą 1100 USD mokėjimą, jei tikite, kad asmuo jums tada mokės.
Laiko vertė ir perkamoji galia
Pinigų laiko vertė taip pat yra susijusi su infliacijos ir perkamosios galios sąvokomis. Reikia atsižvelgti į abu veiksnius, taip pat į tai, kokia grąža gali būti pasiekta investuojant pinigus.
Kodėl tai svarbu? Nes infliacija nuolat ardo pinigų vertę, taigi ir perkamąją galią. Geriausiai tai rodo tokių prekių kaip dujos ar maistas kainos. Pavyzdžiui, jei 1990 m. Jums buvo suteiktas 100 USD nemokamo benzino sertifikatas, galėtumėte nusipirkti daug daugiau galonų dujų, nei galėtumėte gauti, jei po dešimtmečio jums būtų suteikta 100 USD nemokamų dujų.

Investuojant pinigus reikia atsižvelgti į infliaciją ir perkamąją galią, nes norėdami apskaičiuoti realią investicijos grąžą, turite atimti infliacijos lygį iš bet kokios procentinės grąžos, kurią uždirbate iš savo pinigų. Jei infliacijos lygis iš tikrųjų yra didesnis nei jūsų investicijų grąža, net jei jūsų investicija rodo nominalią teigiamą grąžą, jūs iš tikrųjų prarandate pinigus perkamosios galios atžvilgiu. Pvz., Jei uždirbate 10% investicijų, bet infliacijos lygis yra 15%, jūs iš tikrųjų prarandate 5% perkamosios galios kiekvienais metais (10–15% = –5%).
Pinigų formulės laiko vertė
Laiko pinigų vertė yra svarbi sąvoka ne tik asmenims, bet ir priimant verslo sprendimus. Įmonės atsižvelgia į pinigų vertę, priimdamos sprendimus dėl investicijų į naujų produktų kūrimą, naujos verslo įrangos ar įrenginių įsigijimą ir kredito sąlygų nustatymą. Pirkimo ir pardavimo sutartis yra svarbiausių komercinių ir kainų derybų rezultatas. Iš esmės jame išdėstyti sutarti sandorio elementai, įtraukta daug svarbių apsaugos priemonių visoms susijusioms šalims ir numatyta teisinė bazė užbaigti turto pardavimą. parduoti savo produktus ar paslaugas.
Skaičiuojant formulę galima naudoti konkrečią formulę būsima vertė pinigų, kad juos būtų galima palyginti su dabartine verte:
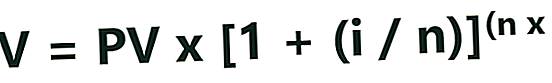
Kur:
FV = būsima pinigų vertė
PV = dabartinė vertė
i = palūkanų norma ar kita grąža, kurią galima uždirbti už pinigus
t = metų, į kuriuos reikia atsižvelgti, skaičius
n = sudedamųjų palūkanų laikotarpių skaičius per metus
Naudodami aukščiau pateiktą formulę, pažvelkime į pavyzdį, kai turite 5000 USD ir galite tikėtis uždirbti 5% palūkanų už šią sumą kiekvienais metais ateinančius dvejus metus. Darant prielaidą, kad palūkanos didinamos tik kasmet, būsimą jūsų 5000 USD vertę šiandien galima apskaičiuoti taip:
FV = 5 000 USD x (1 + (5% / 1) ^ (1 x 2) = 5 512,50 USD
Dabartinė būsimų pinigų formulės vertė
Formulę taip pat galima naudoti apskaičiuojant dabartinė vertė pinigų, kuriuos reikės gauti ateityje. Jūs paprasčiausiai padalysite būsimą vertę, o ne padauginsite dabartinę vertę. Tai gali būti naudinga atsižvelgiant į dvi skirtingas dabartines ir būsimas sumas. Pirminiame pavyzdyje mes apsvarstėme galimybes kas nors sumokėti jūsų 1000 USD, palyginti su 1100 USD per metus nuo dabar. Jei dabar uždirbdami pinigus galėtumėte uždirbti 5 proc. Ir norėtumėte sužinoti, kokia dabartinė vertė prilygtų būsimai 1100 JAV dolerių vertei, arba kiek pinigų jums prireiks dabar, kad turėtumėte 1100 USD per metus, formulė būtų būti toks:
PV = 1 100 USD / (1 + (5% / 1) ^ (1 x 1) = 1 047 USD
Pirmiau pateiktas skaičiavimas rodo, kad turėdami 5% grąžą per metus, jums reikės gauti 1 047 USD dabar, kad lygi būsimai 1100 USD vertei, kurią gausite po metų.
Kad viskas būtų lengviau, yra keletas internetinių skaičiuoklių, kad būtų galima nustatyti būsimą pinigų vertę ar dabartinę pinigų vertę.
Grynosios dabartinės vertės pavyzdys
Žemiau pateikiama pinigų srautų serijos grynosios dabartinės vertės iliustracija. Kaip matote, būsimoji pinigų srautų vertė pateikiama diagramos viršuje, o dabartinė pinigų srautų vertė rodoma mėlynose juostose palei diagramos apačią.
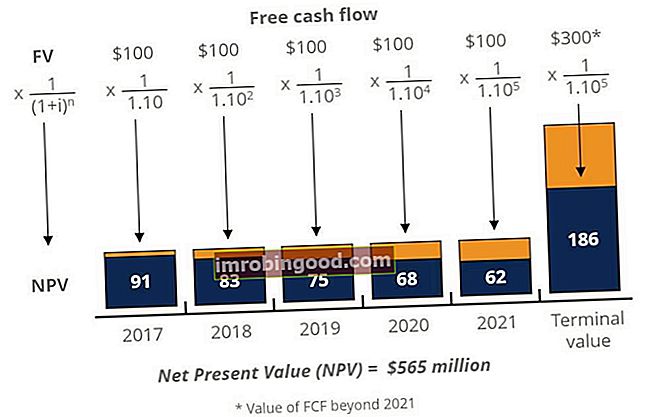
Šis pavyzdys paimtas iš „Finance's Free Corporate Finance“ kurso, kuriame išsamiau aptariama tema.
Papildomi resursai
Tikimės, kad jums patiko Finansų paaiškinimas apie laiko vertę. Norėdami sužinoti daugiau apie pinigus ir investavimą, peržiūrėkite šiuos išteklius:
- Pakoreguota dabartinė vertė Patikslinta dabartinė vertė (APV) Patikslinta dabartinė projekto vertė (APV) apskaičiuojama kaip jo grynoji dabartinė vertė ir dabartinė skolų finansavimo šalutinių poveikių vertė. Peržiūrėkite pavyzdžius ir atsisiųskite nemokamą šabloną. Kodėl verta naudoti koreguotą dabartinę vertę, o ne NPV? Turime suprasti, kaip finansavimo sprendimai (skola prieš nuosavą kapitalą) veikia projekto vertę
- Prognozavimo metodai Prognozavimo metodai Į viršų Prognozavimo metodai. Šiame straipsnyje paaiškinsime keturių rūšių pajamų prognozavimo metodus, kuriuos finansų analitikai naudoja prognozuodami būsimas pajamas.
- NPV formulė NPV formulė NPV formulės „Excel“ vadovas atliekant finansinę analizę. Svarbu tiksliai suprasti, kaip NPV formulė veikia „Excel“ ir už jos esančią matematiką. NPV = F / [(1 + r) ^ n] kur, PV = dabartinė vertė, F = būsimas mokėjimas (pinigų srautas), r = diskonto norma, n = laikotarpių skaičius ateityje
- Vertinimo metodai Vertinimo metodai Vertinant įmonę kaip tęstinę veiklą, naudojami trys pagrindiniai vertinimo metodai: DCF analizė, palyginamos įmonės ir precedentiniai sandoriai. Šie vertinimo metodai naudojami investavimo bankų, nuosavybės tyrimų, privataus kapitalo, įmonių plėtros, susijungimų ir įsigijimų, sverto išpirkimo ir finansų srityse.