Elastinei neto linijinei regresijai regresijos modeliams sureguliuoti naudojamos tiek lazso, tiek kraigo technikos sankcijos. Ši technika sujungia lasą LASSO LASSO, sutrumpintai kaip mažiausiai absoliutus susitraukimas ir atrankos operatorius, yra statistinė formulė, kurios pagrindinis tikslas yra funkcijų parinkimas, reguliavimas ir kraigo regresijos metodai, mokantis iš jų trūkumų, siekiant pagerinti statistinių modelių reguliavimą.
Elastinio tinklo metodas pagerina lasso apribojimus, t. Y. Kai lasas paima kelis pavyzdžius, kad gautų didelių matmenų duomenis, elastinio tinklo procedūra numato „n“ kintamųjų skaičiaus įtraukimą iki prisotinimo. Tuo atveju, kai kintamieji yra labai susijusios grupės, lasasas linkęs pasirinkti vieną kintamąjį iš tokių grupių ir visiškai ignoruoti likusius.
Norint pašalinti lasso nustatytus apribojimus, elastiniame tinkle bausmė apima kvadratinę išraišką (|| β || 2), kuri, naudojant atskirai, tampa kraigo regresija. Kvadratinė bausmės išraiška padidina nuostolių funkciją link išgaubtos. Elastinis tinklas remiasi geriausiu iš abiejų pasaulių - t. Y. Lazso ir kalvagūbrio regresija.
Elastinio tinklo metodo įverčio radimo procedūroje yra du etapai, apimantys ir lazso, ir regresijos metodus. Pirmiausia jis nustato kraigo regresijos koeficientus ir tada atlieka antrą žingsnį, naudodamasis lasso rūšies koeficientų susitraukimu.
Todėl taikant šį metodą koeficientai skirstomi į dviejų rūšių susitraukimus. Dvigubas susitraukimas iš naivios elastingos tinklo versijos sukelia mažą nuspėjamumo efektyvumą ir didelį šališkumą. Norint ištaisyti tokius efektus, koeficientai keičiami, padauginus juos iš (1 + λ2).
Greita santrauka
- Elastinio tinklo metodas vienu metu atlieka kintamąjį pasirinkimą ir reguliavimą.
- Elastinio tinklo technika yra tinkamiausia, kai matmenų duomenys yra didesni už naudojamų mėginių skaičių.
- Grupavimas ir kintamųjų pasirinkimas yra pagrindiniai elastinio tinklo technikos vaidmenys.
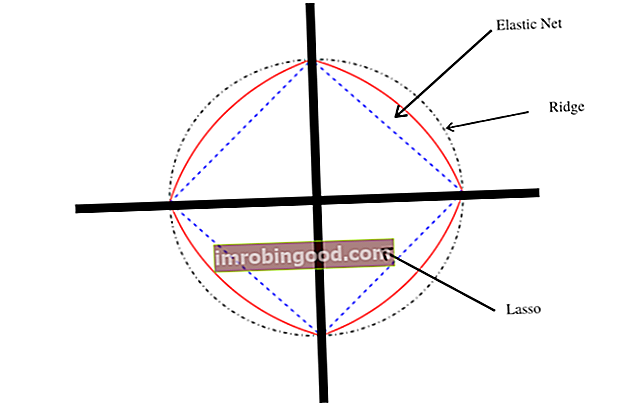
Elastinė tinklo geometrija
Braižant Dekarto plokštumoje, elastinis tinklas patenka tarp kraigo ir laso regresijos diagramų, nes tai yra šių dviejų regresijos metodų derinys. Elastinio tinklo siužetas taip pat rodo unikalumą viršūnėse, kurios yra svarbios retumui. Jis taip pat turi griežtus išgaubtus kraštus, kur išgaubimas priklauso nuo α vertės.
Išgaubtumas taip pat priklauso nuo grupavimo efekto, priklausančio nuo koreliacijos Koreliacija Koreliacija yra statistinis dviejų kintamųjų santykio matas. Ši priemonė geriausiai naudojama kintamuosiuose, kurie rodo linijinį tarpusavio ryšį. Duomenų tinkamumą galima vizualiai pavaizduoti išsklaidytoje schemoje. iš pasirinktų kintamųjų. Kuo didesnė kintamųjų koreliacija, tuo didesnis grupavimo efektas, taigi ir didesnis į imtį įtrauktų kintamųjų skaičius.
Kintamųjų pasirinkimas
Modelio kūrimas reikalauja kintamųjų pasirinkimo, kad susidarytų prediktorių pogrupis. Elastiniame tinkle naudojamas p >> n problemos metodas, o tai reiškia, kad nuspėjamųjų skaičių skaičius yra didesnis nei pavyzdyje naudojamų pavyzdžių skaičius. Elastinis tinklas yra tinkamas, kai kintamieji sudaro grupes, kuriose yra labai koreliuojančių nepriklausomų kintamųjų. Nepriklausomas kintamasis Nepriklausomas kintamasis yra įvestis, prielaida arba variklis, kuris pakeistas siekiant įvertinti jo poveikį priklausomam kintamajam (rezultatui). .
Kintamasis pasirinkimas įtraukiamas į modelio sudarymo procedūrą, kad būtų lengviau padidinti tikslumą. Tuo atveju, kai kintamųjų grupė yra labai susijusi ir vienas iš kintamųjų yra atrenkamas į imtį, visa grupė automatiškai įtraukiama į imtį.
„CATREG“ įkūrimas
CATREG yra algoritmas, palengvinantis kintamųjų transformaciją, tiek tiesinę, tiek netiesinę. Algoritmas naudoja žingsnio ir splaino funkcijas transformuodamas kintamuosius monotoniškai arba monotoniškai netiesinėse transformacijose. CATREG gali vienu metu transformuoti ir reguliuoti kintamuosius ne monotoniškai, nereikalaujant iš pradžių išplėsti kintamuosius į pagrindines funkcijas arba manekeno kintamuosius.
Elastinės grynųjų nuostolių funkcijos taip pat gali būti vadinamos įprasto mažiausių kvadratų regresijos nuostolių funkcijos apribotu tipu. CATREG algoritmas yra integruotas į elastingą tinklą, kuris pagerina gauto algoritmo efektyvumą ir paprastumą. Palyginimui, elastingas tinklas lenkia lasą, kuris pats efektyvumu ir paprastumu lenkia kraigo regresiją.
Elastinio tinklo reguliavimas
Reguliavimo procedūros metu l1 baudos skyrius sudaro negausų modelį. Kita vertus, kvadratinis baudos skyrius daro l1 dalis stabilesnė reguliavimo kelyje, pašalina pasirinktinų kintamųjų kiekio ribą ir skatina grupavimo efektą.
Grupavimo efektas padeda kintamuosius lengvai identifikuoti naudojant koreliaciją. Tai pagerina mėginių ėmimo procedūrą. Tai taip pat padidina pasirinktų kintamųjų skaičių, nes kai vienas kintamasis atrenkamas labai koreliuojančioje grupėje, visi kiti tos grupės kintamieji automatiškai įtraukiami į imtį.
Efektyvūs laisvės laipsniai
Efektyvūs laisvės laipsniai matuoja modelio sudėtingumą. Laisvės laipsniai yra svarbūs vertinant arba tiksliai prognozuojant modelio pritaikymą. Laisvės laipsniai taip pat įtraukiami mokantis linijinių lygintuvų. Bet kokiu metodu, susijusiu su l1 bausmė, nelinijinis modelių pobūdis kelia iššūkį analizėje.
Elastinis tinklas taip pat gali būti naudojamas kitose srityse, pvz., Retame PCA, kur gaunami pagrindiniai komponentai, kuriuos modifikuoja retos apkrovos. Kita programa yra branduolio elastiniame tinkle, kur klasės branduolio mašinos generuojamos su atramos vektoriais.
Papildomi resursai
Finansai siūlo atestuotą bankininkystės ir kredito analitiką (CBCA) grąžinimai ir dar daugiau. sertifikavimo programa tiems, kurie nori pakelti savo karjerą į kitą lygį. Norėdami toliau mokytis ir plėtoti savo žinių bazę, ištirkite toliau nurodytus papildomus atitinkamus finansų išteklius:
- Sprendimų medis Sprendimų medis Sprendimų medis yra pagalbinė priemonė, kurios struktūra panaši į medį, kuri modeliuoja tikėtinus rezultatus, išteklių kainą, komunalines paslaugas ir galimas pasekmes.
- Priklausomas kintamasis Priklausomas kintamasis Priklausomas kintamasis yra tas, kuris pasikeis priklausomai nuo kito kintamojo, vadinamo nepriklausomu kintamuoju, vertės.
- Daugybinė tiesinė regresija Daugkartinė tiesinė regresija Daugkartinė tiesinė regresija reiškia statistinę metodiką, naudojamą prognozuoti priklausomo kintamojo rezultatą, remiantis nepriklausomų kintamųjų verte.
- Overfitting Overfitting Overfitting yra terminas, vartojamas statistikoje, nurodantis modeliavimo klaidą, kuri atsiranda, kai funkcija per daug atitinka tam tikrą duomenų rinkinį